The objective of this study was to estimate the impact of some factors on heritability estimates of body weight (BW), feed conversion ratio (FCR), feed intake (FI), age at first egg (AFE), egg production (EP) and egg weight (EW). Data were possessed from 75 peer reviewed scientific papers published in 1986–2015 years.
Introduction
Over the last decades, a number of genetic parameter estimates for chicken traits have been reported in literature. It is suspected that these estimates vary across populations, time as well as statistical methods and models. The objective of this study was to estimate the impact of some factors on heritability estimates of body weight, feed conversion ratio, feed intake, age at first egg, egg production and egg weight.
Material and methods
The heritabilities of the following chicken traits were studied: body weight (BW), feed conversion ratio (FCR), feed intake (FI), age at first egg (AFE), egg production (EP) and egg weight (EW).
Data were extracted from 75 peer reviewed scientific papers published in the years 1986–2015 by the following scientific journals: Archiv Tierzucht, ARPN Journal of Agricultural and Biological Science, BMC Genetics, BMC Genomics, British Poultry Science, Canadian Journal of Animal Science, Genetics and Molecular Biology, Genetic and Molecular Research, Genetics Selection Evolution, Indian Journal of Animal Research, Journal of Animal and Poultry Sciences, Indian Journal of Animal Sciences, Iranian Journal of Applied Animal Science, Journal of Animal Breeding and Genetics, Journal of Applied Genetics, Journal of Applied Poultry Research, Life Science Journal, Livestock Production Science, Livestock Research for Rural Development, Livestock Science, Nigerian Journal of Animal Production, Poultry Science, Tropical Animal Health and Production as well as literature data (genetic and breeding part) collected for the ECO-FCE project.
The heritability estimates were classified (depending on traits) according to: breed (commercial and local ones), size of population (linear covariable), sex (males, females and combined analyses), trait recording period (linear covariable), statistical method (Gibbs sampling, REML and others) and models (unitrait sire, sire and dam animal and random/fixed models, multitrait models). More details on structure of the data are given in Table 2.
Three approaches were applied: analysis of variance with Tukey’s honest significance post-hoc test, multiple regression equations, and 95% and 99% confidence intervals for expected values of heritabilities were constructed. General formula of the linear model is as follows:
Yijkl…= µ + Bi + Sj + mk + Ml + b1p(w)i + b2Nijk +(BS)ij + (Bm)ik + (BM)il + (Sm)jk + (SM)jl + (mM)kl+eijkl
where: yijk – observed heritability estimate; µ – overall mean; Bi – fixed effect of breed; Sj – fixed
effect of sex (in the case of egg production traits, the effect is omitted); mk – fixed effect of model; Ml – fixed effect of method; p(w)iijkl – size of population included as linear covariable; Nijkl – period included as linear covariable (for some traits, only); b1 and b2 – partial linear regression coefficients for size of population and recording period, respectively; (BS)ij – fixed effect of interaction between breed and sex; (Bm)ik – fixed effect of interaction between breed and model; (BM)il – fixed effect of interaction between breed and method; (Sm)jk – fixed effect of interaction between sex and model; (SM)jl – fixed effect of interaction between sex and method; eijkl – random error connected with ijkl-th observations. These computations were performed using the R software (R Development Core Team, 2008).
Results and discussion
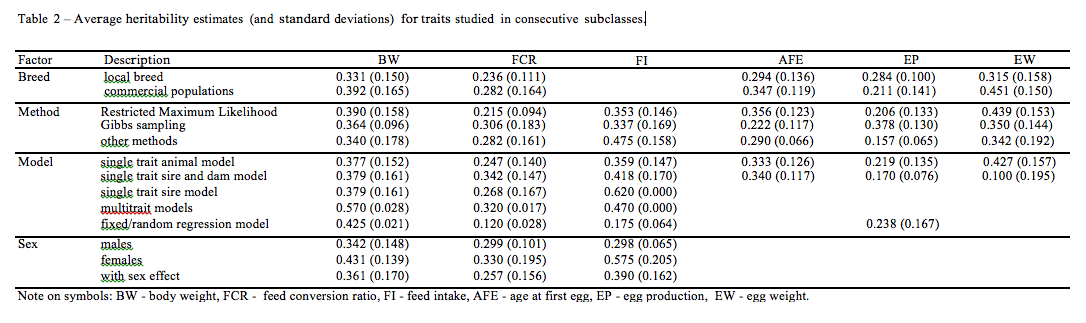
Confidence intervals for expected value with significance level of 0.05 and 0.01 were estimated for each trait (Table 1).
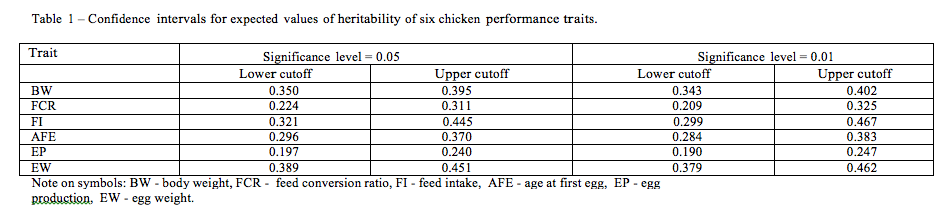
Generally, the sizes of subclasses within the factors varied. As expected, a majority of reports (for all traits) were performed in the commercial populations. The methodology was usually based on restricted maximum likelihood under a single trait animal model (with direct additive genetic effects). Basic characteristics of the influence of the factors studied on heritability estimates (including standard deviations) are given in Table 2. For a majority of traits the higher heritabilities were estimated for commercial populations compared to local flocks. It is probably connected with both number of reports and population sizes. In the case of FCR and EW, the highest estimates of h2 (and statistically significant) were estimated via a Gibbs sampling approach. On the other hand, for BW, AFE and EW higher h2 were received via REML, whereas for FI by other methods. However, it is well known that precision of parameter estimates depends on the assumption of the statistical models. When an empirical normal distribution does not hold, the residual variance is overestimated. It leads to underestimation of heritability coefficients. Unfortunately, the effects of data transformation are not examined here. In turn, omission of the important effect from the model affects the magnitude of the variance components. The effects of the linear model are quite different for the traits analyzed. Several comparative studies on Gibbs sampling and REML estimates in chicken have been performed by other authors as well as in other livestock populations. Bayesian estimates were usually higher than REML ones. However, the reported dependencies were considerably determined by population specific and statistical modeling of the traits. Also some differences in heritabilities were observed among males and females, and combined analysis of both of them. It should be stressed that interactions between some fixed effects were statistically significant. For instance, in the case of AFE, an interaction between breed and the linear model was statistically significant (p=0.017). It confirms the need for specification of the statistical model for a given population. Also both covariables (population size and recording period) were significantly affected by the magnitude of heritability estimates. Generally, the results obtained via the analysis of variance correspond with the ones found on the basis of multiple regression.
Conclusions
Generally, the results indicate statistically significant effects of studied factors on magnitudes of heritability estimates. The performed study shows the importance of correct statistical modeling in the estimation of genetic parameters.
References are available on request
From the Proceedings of the 6th Mediterranean Poultry Summit